I read a blog post at Rebecca Zook’s Blog,Zook Tutoring, about “Building a better teacher.” She says…
…to teach math well, you need to know math, and you need to know how to teach. But there’s a third, separate body of knowledge – knowing how to teach math.
She states that there are special skills needed to teach to a classroom of 30 students, each at a different level, and each with a different learning style, etc.
In Green’s words, “Teaching, even teaching third-grade math, is extraordinarily specialized, requiring both intricate skills and complex knowledge about math. … Mathematicians need to understand a problem [not] only for themselves; math teachers need both to know the math and how 30 different minds might understand (or misunderstand) it.” Green describes, “At the heart of M.K.T. [“mathematical knowledge for teaching.”]… was an ability to step outside your own head. ‘Teaching depends on what other people think,’ Ball told me, ‘not what you think.’”
RIGHT ON!!! I think about this every day!
The foundation of my teaching philosophy is that each person’s brain is different, and my job is to help get math into your brain — even if it works completely different from mine.
This really makes each teacher’s job even more complex.
If everyone (or the people in charge of education and educational funding) knew how complex this job is, there would be more money spent on teachers and educating teachers properly.
Right now we are just turning out widgets (teachers) for the most part.
When a truly exceptional teacher comes along, it is a miracle. This person seems to know innately what it takes and isn’t teaching from what was learned at a teacher’s college.
An example of teaching what makes sense to each student is the Gallon Man.
I first learned about the Gallon Man when I was tutoring students, preparing them to take the state End of Grade tests. Some of the educational coaches for the students with disabilities taught me and also their students about the Gallon Man and other strategies to help them pass these tests.
Here is a drawing of the Gallon man. If you want to know more about it go to Rebecca Zook’s Blog,Zook Tutoring, to see the full explanation. See the G for gallon, Q for quarts, P for pints, C for cups and the 8 ounces.

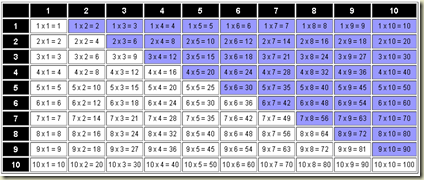
Another strategy for these students was the multiplication chart.
Students are all given a piece of graph paper (and as many more as they need) to use for the EOG math tests.
Students are taught, by their coaches, how to lay out the multiplication tables grid. This helps those who don’t know their multiplication tables quickly to prepare an aid for getting those answers fairly easily.
Here is a color coded example.
Here is a plain example that students can recreate on the graph paper allotted to them.
Here is an example that shows that you only need to learn half of the tables.
These are all strategies for students to help them in math. Each student learns differently and each student can use or make aids that will help them learn best.
Teachers need to be able to find these strategies for each student. They also need to involve the students in finding these strategies, these ways to make sense of math.
Sal Kahn,The Kahn Academy, mentioned in an earlier post, agrees that students need to take time to understand what this learning concept means, not just do a problem and get the right answer. Once true understanding of the concept is earned, then the next step in math is easier, etc.
HOW do you make sure EACH of your students understands the concept? Leave a comment.
[As always, in my author quotes, the underlines, color changes, and bold type is mine, not the author’s!]





 Digg/fivbert
Digg/fivbert Flickr/fivbert
Flickr/fivbert Myspace/fivbert
Myspace/fivbert Facebook/fivbert
Facebook/fivbert Twitter/fivbert
Twitter/fivbert YouTube/fivbert
YouTube/fivbert Del.icio.us/fivbert
Del.icio.us/fivbert Wikipedia/fivbert
Wikipedia/fivbert GMail/fivbert
GMail/fivbert Technorati/fivbert
Technorati/fivbert Blog/fivbert
Blog/fivbert
1 comment:
Thanks so much for writing about my blog and Gallon Man!! I enjoy reading your reflections.
To answer your question, "how do you know when a student understands the concept instead of just the procedure" -- I'm still trying to figure this out myself!
One useful way I've found to assess is to ask the student to teach it back to you. If they do get the concept, they'll usually articulate it.
Sometimes I find students just want to know "how" to do it instead of why, but I really try to teach them why so they can recreate what to do if they forget "how"!
Post a Comment